Chapter 1

Abstract

Commute time is a critical but underrepresented factor in online real estate search platforms. While existing systems offer location-based filtering via radius constraints or isochrone maps, they fail to provide exact travel times for individual listings. We address this gap by developing efficient algorithms that compute and filter real estate listings based on exact commute times to a given destination within a specified time budget. Formally, we model the road network as a weighted graph and compute, for a query point and time budget, all listings that can reach the query point and their precise travel times. Our work makes several key contributions: we extend and adapt classical shortest path algorithms: Dijkstra's algorithm, Dial's algorithm, full precomputation, Contraction Hierarchies, and Hub Labeling, to efficiently handle queries that return travel times from any listing to a fixed destination, accounting for both preprocessing constraints and memory usage. We also provide a rigorous theoretical analysis of each method, assessing runtime and memory requirements in the context of commute-time queries. In addition, we present a detailed experimental evaluation on large real world urban networks, revealing practical trade-offs between preprocessing time, query speed, and memory footprint. These insights demonstrate how exact commute time filtering can be integrated into interactive real estate platforms while achieving fast, scalable performance.

Related Work

There are generally two popular methods currently used to filter by commute time. Both methods work by first determining a geometric object that represents the users interested search area over the map and then filtering objects based on their inclusion in the search area.

1. Radius Based Filtering: Flatfox uses a radius based approach to filter locations based on the user's desired radius of interest. A user sets a starting point and a radius, and the system filters locations within that radius. This method is intuitive and easy to use, but as can be seen by the next method, it may not be accurate for all types of locations.
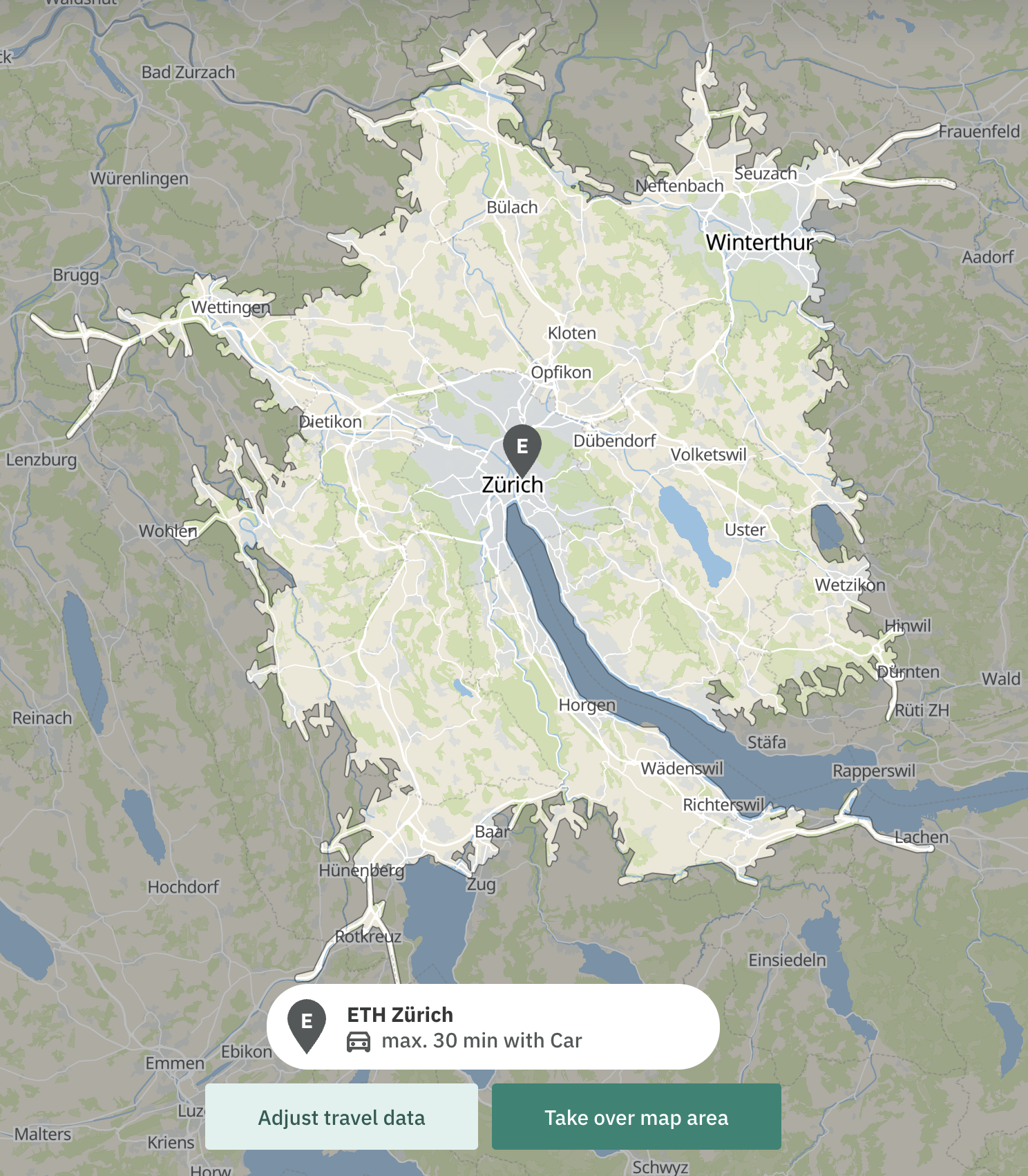
2. Isochrone Maps: Newhome precomputes all regions of the map that are reachable within a certain time from a given point. This method, commonly referred to as isochrone maps [Allen2018, page 2], is more accurate than radius based filtering, as it takes into account the actual travel time between locations. As can be seen in the image below, the isochrone map provides a more accurate representation of the reachable areas compared to the radius based filtering.

Both of these approaches have a common problem. While it is possible to filter based on the commute time, there is no way of knowing the exact time it will take to reach a listing. One can only know that the travel time will be within a certain range. While this is helpful, a potential appartment that is only 5min away might be considerably more interesting than one that is 25min away, even if both are within the permissible range.

Further the more complex the geometric shape of the area, the more computationally expensive it becomes to determine if a location is within the object's boundaries. Consider also that there may be holes within the object's boundaries.

Problem Definition

Given the following inputs:

• A weighted graph $G = (V, E, w)$ defined as:
  • $V$ is the set of vertices. Each $v \in V$ represents one of the following:
    • a road intersection,
    • or a listing location,
  • $E$ is the set of edges, where each $e = (u, v) \in E$ connects two vertices $u, v \in V$ and represents a road segment.
  • $w: E \to \mathbb{N}_0$ is a weight function where $w(e)$ denotes the travel time in seconds to traverse edge $e$.
• A query point $q \in V$ representing the commute destination.
• A finite set $L \subseteq V$ representing the locations of apartments or houses on offer (listings).
• A travel time function $t: V \times V \to \mathbb{N}_0$ defined as:
  $$t(x, y) := \min_{r: x \to y} \sum_{e \in r} w(e)$$

  where the minimum is taken over all paths $r$ from $x$ to $y$ in the graph $G$.

• A time budget $B \in \mathbb{N}_0$ specifying the maximum allowed commute time in seconds.

The goal is to compute the set of pairs $S$, where:

In other words: For each listing location $l \in L$ that can reach the query point $q$ within the time budget $B$, compute both the listing $l$ and the travel time $t(l, q)$.